SubnetDAS – an intermediate DAS approach
By Francesco and Ansgar. Thanks to Mark Simkin for discussions and help in the security analysis, and to various members of the EF research team for feedback.
This is a subnet-based DAS proposal, meant to bridge the gap between EIP-4844 and full Danksharding, much like peerDAS. We propose a DAS construction where there is a subnet for each sample, and nodes get their samples by connecting to them. We think that it can give us more scale without jeopardizing the liveness of the whole network or increasing node requirements compared to EIP-4844.
For this, we do sacrifice something, i.e., unlinkability of queries, or rather the possibility of later addressing this issue within this DAS framework. To retrieve samples, a node has to join the corresponding subnets, and, while attempting to do so, it exposes its queries. This allows an attacker to only publish those samples, thus convincing it that the data is available while it is not. Linkability of queries is a problem faced by all DAS constructions, but it is particularly hard to see how it could be solved in a subnet-based one. It does not affect the availability guarantees of the whole chain, and thus the safety of rollups, but it does weaken the safety of full nodes against double spends. We discuss this issue in detail later, and argue that this weakening is not as significant as it may seem, and that it might be a sensible trade-off for an intermediate DAS solution.
Why SubnetDAS
There’s a few reasons why we think that subnets are a sensible candidate for the main networking structure of an intermediate solution:
- Little networking unknowns: Subnets are a tried and tested piece of the Ethereum networking infrastructure, as attestation subnets have been used since day one of the Beacon Chain. The novelty would be that a higher number of subnets is used, but this would be counterbalanced by full nodes joining in multiple subnets each, so that each subnet should still contain sufficiently many nodes.
- Scale: with bandwidth requirements similar to EIP-4844, we think subnetDAS can achieve similar scale to full Danksharding. With the example parameters we give later, the througput would be 16 MiBs per slot, while requiring full nodes to participate in subnets whose total data assignment is 256 KiBs per slot, and validators 512 KiBs per slot, roughly in line with 4844.
-
Future-compatibility: we think that the subnet infrastructure will be used even in future iterations of DAS, so that the effort is reusable:
- Whatever the final networking construction for DAS might be, the networking structure of full Danksharding will likely involve subnets where rows and columns of the Danksharding square are distributed and which at least validators join to download the rows and columns they are assigned to custody (this is also assumed in peerDAS)
- Even in a later iteration, it might still make sense to use some form of subnetDAS for the fork-choice of validators, which does not need to use the same DAS construction that full nodes use in their fork-choice, to follow the chain and confirm transactions (see here for details). When used for this purpose, the weaknesses of subnetDAS are acceptable or irrelevant:
- Linkability of queries does not matter, because for the fork-choice of validators we only care about global availability guarantees instead of individual ones (there’s no concerns about double spend protection, as this is not used to confirm transactions).
- Validators can be expected to have higher bandwidth requirements than full nodes, so even for the long term it is probably ok to keep bandwidth requirements similar to 4844 for validators.
- Even in a later iteration, it might alternatively make sense to use subnetDAS as a fork-choice filter, while some additional sampling is used only as part of the confirmation rule (again, see here for details). For example, full nodes could follow the chain (and validators participate in consensus) by only using subnetDAS for their fork-choice, while doing some peer sampling only to confirm transactions. A liveness failure of peer sampling would then only affect a full node’s ability to confirm transactions, leaving the p2p network, consensus and the transaction confirmations of super full nodes unaffected. This additional sampling could even be optional, letting full nodes choose their own tradeoff between confirmation safety and liveness. As in the previous bullet point, linkability of queries would not matter because of the additional sampling done as part of the confirmation rule.
Construction
Example parameters
| Parameter | Value | Description |
|---|---|---|
| b | 128 | Number of blobs |
| m | 2048 | Number of column subnets = Number of samples |
| k | 16 | Samples per slot = column subnets per node |
| r | 1 | Row subnets per validator |
Blobs are 128 KiBs, as in EIP-4844, for a total throughput of 16 MiBs per slot of non-extended data.
Data layout
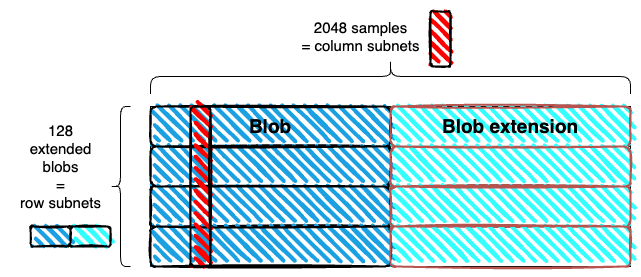
- We use a 1D extension, instead of 2D. The blobs are extended horizontally and stacked vertically. As in the Danksharding matrix, but without a vertical extension.
- The resulting rectangle is subdivided into m columns. With the example parameters, each column is of width 4 field elements (each extended blob is 256 KiBs, or 8192 field elements). Each column is a sample. With the example parameters, a sample has size 128*4*32 bytes = 16 KiBs
Subnets
- Column subnets: Each column (sample) corresponds to a column subnet. Column subnets are used for sampling, and all full nodes connect to k of them.
- Row subnets: Each row (an extended blob) corresponds to a row subnet, which is used for reconstruction. Only validators need to connect to row subnets, and they connect to r of them.
With the example parameters, each column subnet has k/m = 1/128 of all full nodes, and each row subnet has r/n = 1/128 of all validators
Distribution
Blobs are distributed in the row subnets and samples in the column subnets, at the same time.
Sampling
Full nodes query k samples per slot, by connecting to the corresponding subnets. This is just sampling over a 1D extension, but where the samples are “long” (columns instead of points).

With the example parameters, this is a total of 16^2 = 256 KiBs, even lower than EIP-4844 (for validators there’s the added load of downloading r=1 extended blob from a row subnet, for an extra 256 KiBs).
Subnet choice and data retrievability
Data retrievability within the retention period raises similar questions as here. To address them, rotation of the subnets can be staggered and happen in the timescale of the data retention period. The effect of doing so in subnetDAS is quite different than in peerDAS, because the choice of subnets is the choice of samples, so not rotating the choice of subnets every slot means always sampling the same indices.
To address this, we could have nodes connect to 2k subnets instead, k stable ones and k which are rotated every slot. Connecting to the former is purely to help with subnet density and data retrievability, while the latter are actually for sampling. Nonetheless, subnetDAS is anyway particularly vulnerable to linkability of queries, so even a stable choice of subnets might make sense in this context.
Reconstruction
Local reconstruction can happen in row subnets. If some data is missing in a row subnet but exists in a column subnet, validators that are in both subnets gossip the missing data in the row subnet. Once > 50% of the extended blob is available, all validators in the row subnet reconstruct it locally, and then carry to their column subnets any data from this row which they are missing.
Security
We analyze two aspects of the security of this construction (again, see here for more details on the security notions):
- Global safety: except with negligible probability, unavailable data is refuted by all except a small minority of full nodes (concretely, we can set a maximum tolerable fraction of full nodes which might not refute unavailable data).
- Client safety: a client cannot be convinced that unavailable data is available, except with negligible probability.
These parallel the two roles of full nodes: contributing to enforce the rules of the network, and allowing trust-minimized interaction with the chain. The first security property is what allows full nodes to contribute to enforce the rules of rollups built on Ethereum, ultimately guaranteeing their safety, under the assumption that a chain which is only seen as canonical by a small minority of full nodes could never end up becoming the Ethereum chain, even if all validators were malicious. Importantly, this holds even if the adversary knows all the queries in advance.
Client safety and query unlinkability
The second notion is quite a bit stronger: we require that no sampling node can be tricked at all (except with negligible probability). To achieve it, we cannot assume that the adversary knows all queries in advance. In fact, it requires query unlinkability, the ability to hide that a set of queries comes from the same node/actor, because without that an adversary can always only make available exactly the data that a single node asks for.
Why do we want this stronger safety notion, if rollups are safe with the weaker one (global safety), and the whole point of a data availability is for it to be used by rollups? This is because the DA layer is tighly coupled with the rest of the Ethereum chain: full nodes simply ignore a chain where some blob data is not available. Tricking a full node into thinking that unavailable data is available can then subject them to a safety violation, i.e., a double spend: they confirm a transaction in a valid chain which looks safe and available, but which is actually unavailable and therefore does not end up being the canonical Ethereum chain. This holds for the confirmation of Ethereum transactions as well as rollup transactions, since rollup state is derived from the canonical Ethereum chain.
Ethereum transactions
I would argue that introducing DAS without query unlinkability does not change the security of Ethereum full nodes against double spends too much. There are two cases, bases on which confirmation rule a full node uses to begin with:
- Synchronous confirmation rule: these nodes do not wait for finality, and instead use a rule (e.g. this one) which makes synchrony assumptions and honest majority assumptions. If the latter are not satisfied (i.e. in a 51% attack), then the rule is anyway unsafe, and double spends can happen. If the latter is satisfied, we are guaranteed that the confirmed chain is available, because only a small portion of honest validators can be tricked into voting for an unavailable chain. In other words, an honest majority can only be slightly weakened due to DAS failures. Therefore, the synchronous confirmation rule is still safe under the same assumptions it requires without DAS.
- Finality: if a node waits for finality today, it gets the assurance that it will not be subject to a double spend unless there are two conflicting finalized blocks, which requires 1/3 of the validator set to commit a slashable offense. With DAS, it is also possible that a finalized block simply is not available, without there being a conflicting finalization. Note that this still requires nearly a malicious supermajority, again because only a small portion of honest validators could be convinced to vote for an unavailable chain. On the other hand, it does not seem to give economic finality guarantees against double spends. A full node might fail to recognize the finalized chain as not available, and confirm a transaction in it. If it never becomes available, social consensus would eventually have to intervene and coordinate a fork starting from a fully available chain, resulting in a safety violation for the full node. In principle, this does not need to involve any slashing, negating any economic finality. In practice, social consensus could choose to slash any validator which voted to finalized the unavailable chain and which fails to produce the data they were supposed to custody by a certain deadline. If the chain really turns out to be unavailable, this would mean that nearly a supermajority of validators has failed to produce their custodied data, and is liable to be slashed.
Moreover, keep in mind that running a super full node which downloads all the data would be an option, and certainly not a prohibitively expensive one for those who transact a lot of value and want the same exact security guarantees against double spend that a full node has today. It is perhaps at least worth discussing whether this (in our opinion minor) security reduction in the transaction confirmation security of full nodes is truly a hill to die on.
Rollup transactions
The picture for the security when confirming rollup transactions is quite similar, but with a few more considerations centered around validity, again depending on which confirmation rule the rollup node is using. Let’s assume that the baseline confirmation rule is Ethereum finality, which is then enhanced with some rollup-specific conditions.
For a validity rollup, the sensible choice is clearly to wait for a validity proof before confirming, though not necessarily for it to be posted and verified on Ethereum itself. Such a node does indeed get the same exact security guarantees that an Ethereum full node gets when confirming a finalized transaction (modulo issues with the proof system or the implementation of the verifier), since validity is guaranteed. In other words, the only attack vector is a double spend of the same kind we have discussed in the previous section.
For an optimistic rollup, there are multiple options. One could run a rollup full node and simply verify all state transitions, in which case clearly there are no extra concerns. This is of course not ideal since rollup nodes could in principle be much heavier than Ethereum nodes. It could also just wait for the rollup bridge to confirm the transaction, which is equally safe but would require a longer confirmation period due to the fraud proof period. Another alternative is to listen for (messages initiating) fraud proofs on a p2p network, which could be done with a shorter fraud proof period than what is appropriate for the bridge. A node operating such a fast confirmation rule could in principle be induced to confirm an invalid transaction if unavailable data is finalized and it is tricked into thinking it is available.
Global safety
Tldr: even an adversary that knows all queries in advance cannot convince more than a small percentage of sampling nodes that unavailable data is available
For an adaptive adversary, which considers all queries at once before deciding which data to make available, the probability that a fraction \epsilon of n nodes is successfully targeted when downloading k samples out of a total of m can be union-bounded by \binom{n}{n\epsilon}\binom{m}{m/2} 2^{-kn\epsilon}: the adversary chooses a subset of n\epsilon nodes, out of \binom{n}{n\epsilon} possible subsets, a subset consisting of at least \frac{m}{2} samples to not make available, out of \binom{m}{m/2} such subsets, and given these choices has a success probability of 2^{-kn\epsilon}. Approximating the binomial cofficients, we get \left(\frac{2^{n}}{\sqrt{\frac{n\pi}{2}}}e^{-\frac{\left(n\ -\ 2n\epsilon\right)^{2}}{2n}}\right)\frac{2^{m}}{\sqrt{\frac{m\pi}{2}}}2^{-kn\epsilon} = \left(\frac{2^{n}}{\sqrt{\frac{n\pi}{2}}}e^{-\frac{\left(n\ -\ 2n\epsilon\right)^{2}}{2n}}\right)\frac{2^{\left(m-kn\epsilon\right)}}{\sqrt{\frac{m\pi}{2}}}, and we want this to be < 2^{-30} or something like that. That gives us (n + m - kn\epsilon) - \log_{2}\left(e\right)\frac{n\left(1\ -\ 2\epsilon\right)^{2}}{2} < \log_2(\sqrt{nm}\frac{\pi}{2})-30
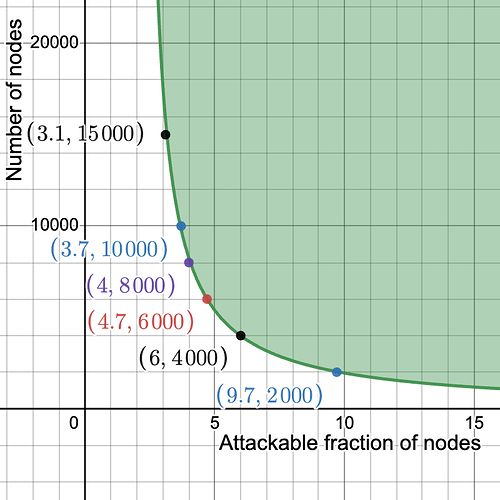
In the following plot, we set k = 16 and m = 2048. On the y-axis we have n, the number of nodes, and on the x-axis \epsilon, the maximum fraction of nodes which can be tricked (here in particular with probability \ge 2^{-30}, but the result is almost insensitive to the chosen failure probability). As long as we have at least 2000 nodes, less than 10% of the nodes can be fraudulently convinced of the availability of data which is not available. Moreover, the fraction of attackable nodes drops between 5% and 4% between 6000 and 10000 nodes.
(You can play with the parameters here)
It is perhaps worth noting that the full Danksharding sampling with m = 512^2 (sampling on the square) and k = 75 does not do better in this kind of analysis, which considers an adversary that knows all of the queries in advance. In fact, it fares much worse, simply due to how large m is. This should not come entirely as a surprise, since nodes in this construction are required to download a much bigger portion of the data (0.256 KiBs/32 MiBs, or 1/128, vs 37.5 KiBs/128 MiBs, or ~1/3000). That said, this is just a bound which might not be tight, so a bad bound does not necessarily imply bad security. If on the other hand the bound were shown to be tight, it would mean that global safety with such a high m does not hold against a fully adaptive adversary, and instead requires some assumption about unlinkability of queries as well.
Security-Throghput-Bandwidth tradeoff
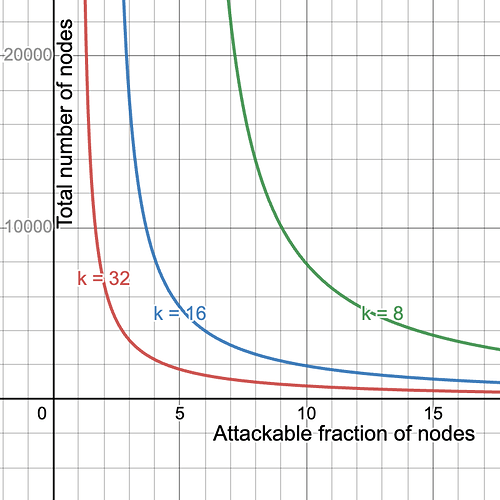
Naturally, we could improve any of bandwidth requirements, security and throughput by worsening one or both of the other two. For example, halving the number of blobs to b = 64 and doubling the number of samples to k=32 would keep the bandwidth requirement the same while halving the throughput, but give us a much better security curve. On the other hand, we could double the throughput while keeping the bandwidth requirements the same, by setting b = 256 and k = 8, sacrificing security. Here we compare the security for k=8,16,32, i.e., corresponding to max throughput 32MiB, 16MiB and 8MiB.
(You can play with the parameters here)